Capital Allocation Line (CAL) und optimales Portfolio

Die Capital Allocation Line (CAL) ist eine Linie, die das Risiko-Ertrags-Profil von Vermögenswerten grafisch darstellt. und kann verwendet werden, um das optimale Portfolio zu finden. Der Prozess zum Erstellen der CAL für eine Sammlung von Portfolios wird unten beschrieben.

Erwartete Rendite und Varianz des Portfolios

Der Einfachheit halber, wir werden ein Portfolio mit nur zwei riskanten Assets aufbauen.

Die erwartete Rendite des Portfolios ist ein gewichteter Durchschnitt der erwarteten Renditen der einzelnen Vermögenswerte, und berechnet sich wie folgt:

E(Rp) =w ₁ E(R ₁ ) + w ₂ E(R ₂ )

Wo wir ₁ , w ₂ sind die jeweiligen Gewichte für die beiden Vermögenswerte, und E(R ₁ ), E(R ₂ ) sind die jeweils erwarteten Renditen.

Varianzniveaus werden direkt mit Risikoniveaus übersetzt; höhere Varianz bedeutet höheres Risiko und umgekehrt. Die Varianz eines Portfolios ist nicht nur der gewichtete Durchschnitt der Varianz einzelner Vermögenswerte, sondern hängt auch von der Kovarianz und Korrelation der beiden Vermögenswerte ab. Die Formel für die Portfoliovarianz lautet:

Var(R _P ) =w ² ₁ Var(R ₁ ) + w ² ₂ Var(R ₂ ) + 2w ₁ w ₂ Cov(R ₁ , R ₂ )

Wo Cov(R ₁ , R ₂ ) stellt die Kovarianz der beiden Vermögensrenditen dar. Alternative, die Formel lässt sich schreiben als:

σ ² _P =w ² ₁ σ ² ₁ + w ² ₂ σ ² ₂ + 2ρ(R ₁ , R ₂ ) w ₁ w ₂ σ ₁ σ ₂ , mit ρ(R ₁ , R ₂ ), die Korrelation von R ₁ und R ₂ .

Die Umrechnung zwischen Korrelation und Kovarianz ist gegeben als:ρ(R ₁ , R ₂ ) =Cov(R ₁ , R ₂ )/ σ ₁ σ ₂ .

Die Varianz der Portfoliorendite ist größer, wenn die Kovarianz der beiden Vermögenswerte positiv ist, und weniger, wenn negativ. Da Varianz ein Risiko darstellt, das Portfoliorisiko ist geringer, wenn seine Vermögensbestandteile eine negative Kovarianz aufweisen. Diversifikation ist eine Technik, die das Portfoliorisiko minimiert, indem in Vermögenswerte mit negativer Kovarianz investiert wird.

In der Praxis, wir kennen die Renditen und Standardabweichungen einzelner Vermögenswerte nicht, wir können diese Werte jedoch anhand der historischen Werte dieser Vermögenswerte schätzen.

Die effiziente Grenze

Eine Portfoliogrenze ist ein Diagramm, das alle möglichen Portfolios mit unterschiedlichen Kombinationen der Vermögensgewichtung abbildet. mit den Niveaus der Portfolio-Standardabweichung auf der x-Achse und der erwarteten Portfoliorendite auf der y-Achse.

Um eine Portfoliogrenze zu konstruieren, wir weisen zuerst Werte für E(R ₁ ), E(R ₂ ), stdev(R ₁ ), stdev(R ₂ ), und (R ₁ , R ₂ ). Mit den obigen Formeln, berechnen wir dann die erwartete Rendite und Varianz des Portfolios für jede mögliche Kombination von Vermögensgewichten (w ₂ =1-w ₁ ). Dieser Vorgang kann einfach in Microsoft Excel durchgeführt werden, wie im folgenden Beispiel gezeigt:

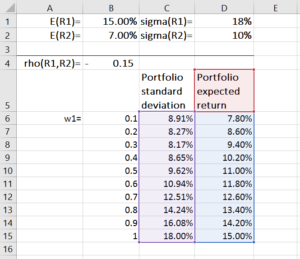
Anschließend verwenden wir das Streudiagramm mit glatten Linien, um die erwartete Rendite und die Standardabweichung des Portfolios darzustellen. Das Ergebnis ist in der folgenden Grafik dargestellt, wobei jeder Punkt auf dem Diagramm ein Portfolio darstellt, das unter einer Kombination von Vermögensgewichten erstellt wurde.

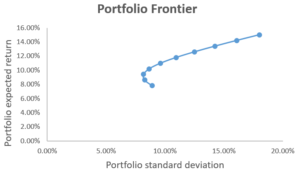
Woher wissen wir also, welche Portfolios für Anleger attraktiv sind? Um dies zu beantworten, Wir stellen das Konzept von . vor Mittelwert-Varianz-Kriterium , die besagt, dass Portfolio A Portfolio B dominiert, wenn E(R _EIN ) ≥ E(R _B ) und σ _EIN ≤ σ _B (d. h. Portfolio A bietet eine höhere erwartete Rendite und ein geringeres Risiko als Portfolio B). Wenn dies der Fall ist, dann würden Investoren A gegenüber B bevorzugen.

Aus der Grafik, wir können folgern, dass Portfolios auf dem abwärts geneigten Teil der Portfoliogrenze vom aufwärts geneigten Teil dominiert werden. Als solche, die Punkte auf dem ansteigenden Teil der Portfoliogrenze stellen Portfolios dar, die Anleger attraktiv finden, während Punkte auf dem nach unten geneigten Teil Portfolios darstellen, die ineffizient sind.

Nach dem Mittelwert-Varianz-Kriterium jeder Investor würde optimalerweise ein Portfolio im aufsteigenden Teil der Portfoliogrenze auswählen, die heißt die Effiziente Grenze , oder minimale Varianzgrenze . Die Wahl eines Portfolios an der Effizienzgrenze hängt von den Risikopräferenzen des Anlegers ab.

Ein Portfolio oberhalb der Effizienzgrenze ist unmöglich, während ein Portfolio unterhalb der Effizienzgrenze ineffizient ist.

Komplette Portfolio- und Kapitalallokationslinie

Beim Aufbau von Portfolios, Anleger kombinieren häufig riskante Vermögenswerte mit risikofreien Vermögenswerten (wie Staatsanleihen), um Risiken zu reduzieren. Ein vollständiges Portfolio ist definiert als eine Kombination aus einem riskanten Anlageportfolio, mit Rücklauf R _P , und der risikolose Vermögenswert, mit Rücklauf R _F .

Die erwartete Rendite eines vollständigen Portfolios wird wie folgt angegeben:

E(R _C ) =w _P E(R _P ) + (1 − w _P )R _F

Und die Varianz und Standardabweichung der vollständigen Portfoliorendite wird wie folgt angegeben:

Var(R _C ) =w ² _P Var(R _P ), (R _C ) =w _P (R _P ),

wo wir _P ist der Anteil, der in das risikoreiche Asset-Portfolio investiert ist.

Während die erwartete Überschussrendite eines vollständigen Portfolios wie folgt berechnet wird:

E(R _C ) - R _F ,

wenn wir E(R _C ) mit der vorherigen Formel, wir bekommen w _P (E(R _P ) − R _F ).

Die Standardabweichung des gesamten Portfolios ist σ(R _C ) =w _P (R _P ), was uns gibt:

w _P =σ(R _C )/σ(R _P )

Deswegen, für jedes komplette Portfolio:

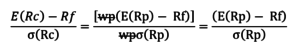
Oder E(R _C ) =R _F + S _P (R _C ), wo ist _P =

Die Linie E(R _C ) =R _F + S _P (R _C ) ist die Kapitalallokationslinie (CAL). Die Steigung der Linie, S _P , heißt der Sharpe-Verhältnis Sharpe RatioDie Sharpe Ratio ist ein Maß für die risikoadjustierte Rendite, die die Überschussrendite einer Anlage mit ihrer Standardabweichung der Renditen vergleicht. Die Sharpe Ratio wird häufig verwendet, um die Wertentwicklung einer Anlage durch Anpassung an ihr Risiko zu messen., oder Chance-Risiko-Verhältnis. Die Sharpe-Ratio misst den Anstieg der erwarteten Rendite pro Einheit zusätzlicher Standardabweichung.

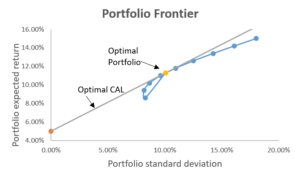
Optimales Portfolio

Das optimale Portfolio besteht aus einem risikofreien Asset und einem optimalen risikoreichen Asset-Portfolio. Das optimale Portfolio mit riskanten Vermögenswerten liegt an dem Punkt, an dem die CAL die Effizienzgrenze berührt. Dieses Portfolio ist optimal, da die Steigung von CAL am höchsten ist, Damit erzielen wir die höchsten Renditen pro zusätzlicher Risikoeinheit. Die folgende Grafik veranschaulicht dies:

Die tangentialen Portfoliogewichte werden wie folgt berechnet:

Zusammenfassung der Kapitalallokationslinie

Anleger nutzen sowohl die Effizienzgrenze als auch die CAL, um je nach Wunsch unterschiedliche Kombinationen von Risiko und Rendite zu erzielen. Das optimale riskante Portfolio wird an dem Punkt gefunden, an dem die CAL tangential zur Effizienzgrenze ist. Diese Kombination aus Vermögensgewichtung ergibt das beste Risiko-Ertrags-Verhältnis, da es die höchste Steigung für CAL hat.

Laden Sie die kostenlose Vorlage herunter

Geben Sie Ihren Namen und Ihre E-Mail-Adresse in das untenstehende Formular ein und laden Sie jetzt die kostenlose Vorlage herunter!

Zusätzliche Ressourcen

Vielen Dank, dass Sie den Leitfaden von CFI zur Kapitalallokationslinie gelesen haben. Um Ihre Karriere als Financial Modeling and Valuation Analyst voranzutreibenWerden Sie Certified Financial Modeling &Valuation Analyst (FMVA)® Die Zertifizierung zum Financial Modeling and Valuation Analyst (FMVA)® von CFI wird Ihnen helfen, das Vertrauen zu gewinnen, das Sie für Ihre Finanzkarriere benötigen. Melden Sie sich noch heute an!, Diese zusätzlichen Ressourcen werden hilfreich sein:

• Portfoliomanagement-KarriereprofilPortfolio-Management-KarriereprofilPortfolio-Management verwaltet Investitionen und Vermögenswerte für Kunden, darunter Pensionskassen, Banken, Hedgefonds, Family Offices bzw. Der Portfoliomanager ist dafür verantwortlich, den richtigen Vermögensmix und die richtige Anlagestrategie aufrechtzuerhalten, die den Bedürfnissen des Kunden entsprechen. Gehalt, Fähigkeiten,
• MarktrisikoprämieMarktrisikoprämieDie Marktrisikoprämie ist die zusätzliche Rendite, die sich ein Anleger durch das Halten eines risikoreichen Marktportfolios anstelle von risikofreien Anlagen erwartet.
• Definition der Sharpe-RatioSharpe-RatioDie Sharpe-Ratio ist ein Maß für die risikoadjustierte Rendite, die die Überschussrendite einer Anlage mit ihrer Standardabweichung der Renditen vergleicht. Die Sharpe Ratio wird häufig verwendet, um die Wertentwicklung einer Anlage durch Anpassung an ihr Risiko zu messen.
• Sharpe-Ratio-RechnerSharpe-Ratio-RechnerMit dem Sharpe-Ratio-Rechner können Sie die risikoadjustierte Rendite einer Anlage messen. Laden Sie die Excel-Vorlage und den Sharpe Ratio-Rechner von CFI herunter. Sharpe-Verhältnis =(Rx - Rf) / StdDev Rx. Wobei:Rx =Erwartete Portfoliorendite, Rf =Risikofreie Rendite, StdDev Rx =Standardabweichung der Portfoliorendite / Volatilität