Hypothesentests im Finanzwesen:Konzept und Beispiele

Ihr Anlageberater schlägt Ihnen einen monatlichen Einkommensanlageplan vor, der jeden Monat eine variable Rendite verspricht. Sie werden nur investieren, wenn Sie ein durchschnittliches monatliches Einkommen von 180 USD haben. Ihr Berater sagt Ihnen auch, dass Sie in den letzten 300 Monaten Das Programm hatte Anlagerenditen mit einem Durchschnittswert von 190 USD und einer Standardabweichung von 75 USD. Sollten Sie in dieses System investieren? Hypothesentests helfen bei einer solchen Entscheidungsfindung.

Die zentralen Thesen

• Hypothesentests sind ein mathematisches Werkzeug zur Bestätigung einer finanziellen oder geschäftlichen Behauptung oder Idee.
• Hypothesentests sind nützlich für Anleger, die versuchen zu entscheiden, in was sie investieren möchten und ob das Instrument wahrscheinlich eine zufriedenstellende Rendite liefert.
• Trotz der unterschiedlichen Methoden der Hypothesenprüfung die gleichen vier Schritte werden verwendet:Definition der Hypothese, die Kriterien festlegen, Berechnen Sie die Statistik, und zu einem Schluss kommen.
• Dieses mathematische Modell, wie die meisten statistischen Tools und Modelle, hat Einschränkungen und ist anfällig für bestimmte Fehler, Dies erfordert, dass Investoren auch andere Modelle in Verbindung mit diesem in Betracht ziehen

Was ist ein Hypothesentest?

Hypothesen- oder Signifikanztests sind ein mathematisches Modell zum Testen einer Behauptung, Idee oder Hypothese über einen interessierenden Parameter in einer gegebenen Populationsmenge, unter Verwendung von Daten, die in einem Stichprobensatz gemessen wurden. An ausgewählten Stichproben werden Berechnungen durchgeführt, um aussagekräftigere Informationen über die Merkmale der gesamten Population zu erhalten, Dies ermöglicht eine systematische Möglichkeit, Behauptungen oder Ideen über den gesamten Datensatz zu testen.

Hier ein einfaches Beispiel:Ein Schulleiter gibt an, dass Schüler in ihrer Schule durchschnittlich 7 von 10 in Prüfungen abschneiden. Um diese „Hypothese zu testen, ” Wir erfassen die Noten von beispielsweise 30 Schülern (Stichprobe) aus der gesamten Schülerpopulation der Schule (z. B. 300) und berechnen den Mittelwert dieser Stichprobe. Wir können dann den (berechneten) Stichprobenmittelwert mit dem (gemeldeten) Grundgesamtheitsmittelwert vergleichen und versuchen, die Hypothese zu bestätigen.

Um ein anderes Beispiel zu nehmen, die jährliche Rendite eines bestimmten Investmentfonds beträgt 8%. Angenommen, der Investmentfonds besteht seit 20 Jahren. Wir ziehen eine Zufallsstichprobe der jährlichen Renditen des Investmentfonds für, sagen, fünf Jahre (Stichprobe) und berechnen den Mittelwert. Anschließend vergleichen wir den (berechneten) Stichprobenmittelwert mit dem (behaupteten) Grundgesamtheitsmittelwert, um die Hypothese zu überprüfen.

Dieser Artikel setzt voraus, dass die Leser mit den Konzepten einer Normalverteilungstabelle vertraut sind, Formel, p-Wert und verwandte Grundlagen der Statistik.

Es gibt verschiedene Methoden zum Testen von Hypothesen, Es sind jedoch die gleichen vier grundlegenden Schritte erforderlich:

Schritt 1:Definieren Sie die Hypothese

In der Regel, der gemeldete Wert (oder die Schadenstatistik) wird als Hypothese angegeben und als wahr angenommen. Für die obigen Beispiele, die hypothese wird sein:

• Beispiel A:Schüler in der Schule erzielen in Prüfungen durchschnittlich 7 von 10 Punkten.
• Beispiel B:Die jährliche Rendite des Investmentfonds beträgt 8% pro Jahr.

Diese angegebene Beschreibung stellt die „ Nullhypothese (H ₀ ) " und ist vermutet um wahr zu sein – die Art und Weise, wie ein Angeklagter in einem Geschworenenprozess für unschuldig gehalten wird, bis seine Schuld durch die vor Gericht vorgelegten Beweise bewiesen wird. Ähnlich, Hypothesentests beginnen mit der Feststellung und Annahme einer „Nullhypothese, “ und dann bestimmt der Prozess, ob die Annahme wahrscheinlich wahr oder falsch ist.

Der wichtige Punkt ist, dass wir die Nullhypothese testen, da Zweifel an ihrer Gültigkeit bestehen. Alle Informationen, die gegen die angegebene Nullhypothese verstoßen, werden im erfasst Alternative Hypothese (H ₁ ). Für die obigen Beispiele, die Alternativhypothese lautet:

• Die Schüler erreichen einen Durchschnitt, der nicht gleich 7.
• Die jährliche Rendite des Investmentfonds beträgt nicht gleich 8% pro Jahr.

Mit anderen Worten, die Alternativhypothese ist ein direkter Widerspruch zur Nullhypothese.

Wie in einem Prozess, die Jury geht von der Unschuld des Angeklagten aus (Nullhypothese). Der Staatsanwalt muss das Gegenteil beweisen (Alternativhypothese). Ähnlich, Der Forscher muss beweisen, dass die Nullhypothese entweder wahr oder falsch ist. Wenn der Staatsanwalt die Alternativhypothese nicht beweisen kann, das Geschworenengericht muss den Angeklagten gehen lassen (Entscheidung auf Basis der Nullhypothese). Ähnlich, wenn der Forscher eine Alternativhypothese nicht beweisen kann (oder einfach nichts tut), dann wird angenommen, dass die Nullhypothese wahr ist.

Die Entscheidungskriterien müssen auf bestimmten Parametern von Datensätzen basieren.

Schritt 2:Legen Sie die Kriterien fest

Die Entscheidungskriterien müssen sich an bestimmten Parametern von Datensätzen orientieren und hier kommt der Bezug zur Normalverteilung ins Spiel.

Gemäß dem Standard-Statistikpostulat über die Stichprobenverteilung, „Für jede Stichprobengröße n, die Stichprobenverteilung von X̅ ist normal, wenn die Grundgesamtheit X, aus der die Stichprobe gezogen wird, normalverteilt ist.“ Somit, die Wahrscheinlichkeiten von alle anderen möglichen Stichprobenmittelwerte die man auswählen könnte, sind normalverteilt.

Für z.B. bestimmen, ob die durchschnittliche Tagesrendite, aller an der XYZ-Börse notierten Aktien, um den Neujahrstag ist größer als 2%.

h ₀ :Nullhypothese:Mittelwert =2%

h ₁ :Alternativhypothese:Mittelwert> 2% (das wollen wir beweisen)

Nehmen Sie die Stichprobe (z. B. von 50 Aktien von insgesamt 500) und berechnen Sie den Mittelwert der Stichprobe.

Für eine Normalverteilung gilt 95 % der Werte liegen innerhalb von zwei Standardabweichungen des Grundgesamtheitsmittels. Somit, diese normalverteilung und zentrale grenzannahme für den Stichprobendatensatz ermöglicht es uns, 5% als Signifikanzniveau festzulegen. Es macht Sinn, da unter dieser Annahme, es besteht eine Wahrscheinlichkeit von weniger als 5 % (100-95), Ausreißer zu erhalten, die über zwei Standardabweichungen vom Mittelwert der Grundgesamtheit liegen. Je nach Art der Datensätze, andere Signifikanzniveaus können mit 1% angenommen werden, 5% oder 10%. Für Finanzberechnungen (einschließlich Behavioral Finance), 5% ist die allgemein akzeptierte Grenze. Wenn wir Berechnungen finden, die über die üblichen zwei Standardabweichungen hinausgehen, dann haben wir einen starken Fall von Ausreißern, um die Nullhypothese abzulehnen.

Grafisch, es wird wie folgt dargestellt:

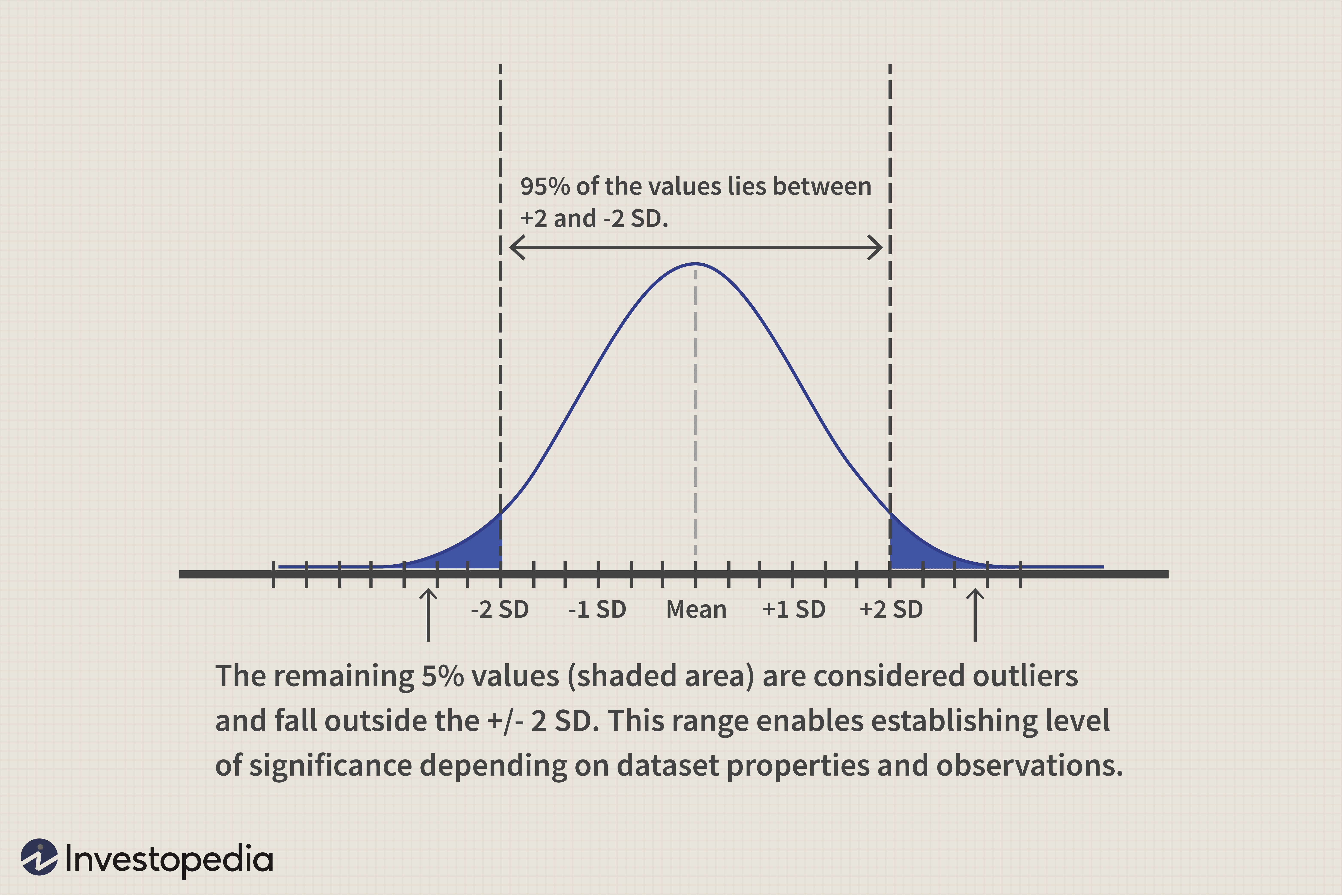
Im obigen Beispiel ist wenn der Mittelwert der Stichprobe viel größer als 2% ist (sagen wir 3,5 %), dann verwerfen wir die Nullhypothese. Die Alternativhypothese (Mittelwert>2%) wird akzeptiert, was bestätigt, dass die durchschnittliche Tagesrendite der Aktien tatsächlich über 2% liegt.

Jedoch, wenn der Mittelwert der Stichprobe wahrscheinlich nicht signifikant über 2 % liegt (und bei sagen, rund 2,2%), dann können wir die Nullhypothese NICHT ablehnen. Die Herausforderung besteht darin, wie in solchen Nahbereichsfällen zu entscheiden ist. Um aus ausgewählten Proben und Ergebnissen eine Schlussfolgerung zu ziehen, ein Signifikanzniveau bestimmt werden soll, was einen Rückschluss auf die Nullhypothese ermöglicht. Die Alternativhypothese ermöglicht es, das Signifikanzniveau oder das Konzept des "kritischen Werts" für die Entscheidung über solche Nahbereichsfälle festzulegen.

Nach der Standarddefinition des Lehrbuchs „Ein kritischer Wert ist ein Cutoff-Wert, der die Grenzen definiert, jenseits derer weniger als 5% der Stichprobenmittelwerte erhalten werden können, wenn die Nullhypothese wahr ist. Über einen kritischen Wert hinaus erhaltene Stichprobenmittelwerte führen zu einer Entscheidung, die Nullhypothese abzulehnen." Im obigen Beispiel gilt:wenn wir den kritischen Wert mit 2,1 % definiert haben, und der berechnete Mittelwert beträgt 2,2 %, dann verwerfen wir die Nullhypothese. Ein kritischer Wert setzt eine klare Abgrenzung zwischen Akzeptanz oder Ablehnung.

Schritt 3:Berechnen Sie die Statistik

Dieser Schritt beinhaltet die Berechnung der erforderlichen Zahl(en), bekannt als Teststatistik (wie Mittelwert, z-Score, p-Wert, etc.), für die ausgewählte Probe. (Wir werden darauf in einem späteren Abschnitt eingehen.)

Schritt 4:Ein Fazit ziehen

Mit dem/den berechneten Wert(en) Entscheiden Sie sich für die Nullhypothese. Wenn die Wahrscheinlichkeit, einen Stichprobenmittelwert zu erhalten, weniger als 5 % beträgt, dann ist die Schlussfolgerung zu ablehnen die Nullhypothese. Andernfalls, annehmen und behalte die Nullhypothese bei.

Arten von Fehlern

Bei der stichprobenbasierten Entscheidungsfindung kann es vier mögliche Ergebnisse geben:im Hinblick auf die korrekte Anwendbarkeit auf die gesamte Bevölkerung:

Entscheidung zu behalten

Entscheidung zur Ablehnung

Gilt für die gesamte Bevölkerung

Richtig

Falsch

(Fehler TYP 1 - a)

Gilt nicht für die gesamte Bevölkerung

Falsch

(Fehler TYP 2 - b)

Richtig

Die „richtigen“ Fälle sind die Fälle, in denen die Entscheidungen über die Stichproben wirklich auf die gesamte Bevölkerung anwendbar sind. Die Fehlerfälle treten auf, wenn man aufgrund der Beispielrechnungen entscheidet, die Nullhypothese beizubehalten (oder abzulehnen), aber diese Entscheidung gilt nicht wirklich für die gesamte Bevölkerung. Diese Fälle stellen Fehler vom Typ 1 (Alpha) und Typ 2 (Beta) dar, wie in der obigen Tabelle angegeben.

Die Auswahl des richtigen kritischen Wertes ermöglicht es, die Alphafehler vom Typ 1 zu eliminieren oder auf einen akzeptablen Bereich zu begrenzen.

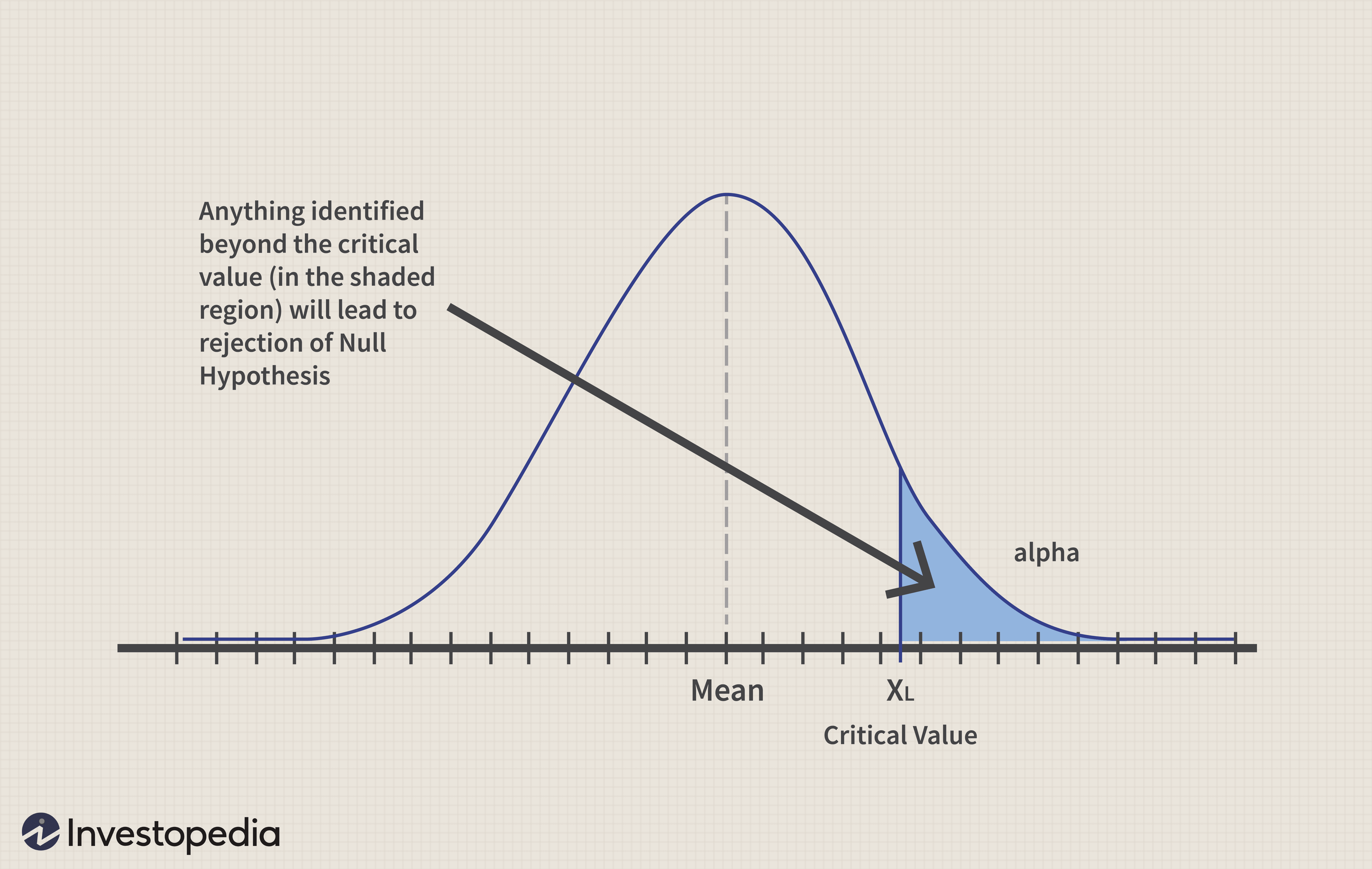
Alpha bezeichnet den Fehler auf der Signifikanzebene und wird vom Forscher bestimmt. Um das standardmäßige Signifikanz- oder Konfidenzniveau von 5 % für Wahrscheinlichkeitsberechnungen beizubehalten, dieser wird bei 5 % beibehalten.

Gemäß den geltenden Entscheidungsmaßstäben und Definitionen:

• „Dieses (Alpha-)Kriterium wird normalerweise auf 0,05 (a =0,05) gesetzt, und wir vergleichen das Alpha-Niveau mit dem p-Wert. Wenn die Wahrscheinlichkeit eines Fehlers vom Typ I weniger als 5 % beträgt (p <0,05), wir beschließen, die Nullhypothese abzulehnen; Andernfalls, wir behalten die Nullhypothese bei.“
• Der Fachausdruck für diese Wahrscheinlichkeit ist der p-Wert . Sie ist definiert als „die Wahrscheinlichkeit, ein Stichprobenergebnis zu erhalten, vorausgesetzt, dass der in der Nullhypothese angegebene Wert wahr ist. Der p-Wert zum Erhalten eines Stichprobenergebnisses wird mit dem Signifikanzniveau verglichen."
• Ein Fehler vom Typ II, oder Beta-Fehler, ist definiert als die Wahrscheinlichkeit, die Nullhypothese fälschlicherweise beizubehalten, obwohl es tatsächlich nicht auf die gesamte Bevölkerung anwendbar ist.

Einige weitere Beispiele werden diese und andere Berechnungen demonstrieren.

Beispiel 1

Es gibt ein monatliches Einkommensanlagesystem, das variable monatliche Renditen verspricht. Ein Anleger wird nur dann investieren, wenn ihm ein durchschnittliches monatliches Einkommen von 180 USD zugesichert wird. Der Anleger hat eine Stichprobe von 300-Monats-Renditen mit einem Mittelwert von 190 USD und einer Standardabweichung von 75 USD. Sollten sie in dieses System investieren?

Stellen wir das Problem auf. Der Anleger wird in das Programm investieren, wenn ihm die vom Anleger gewünschte durchschnittliche Rendite von 180 USD zugesichert ist.

h ₀ :Nullhypothese:Mittelwert =180

h ₁ :Alternativhypothese:Mittelwert> 180

Methode 1: Critical-Value-Ansatz

Identifizieren Sie einen kritischen Wert X _L für den Stichprobenmittelwert, die groß genug ist, um die Nullhypothese abzulehnen – d. h. die Nullhypothese abzulehnen, wenn der Stichprobenmittelwert>=kritischer Wert X _L

P (identifiziere einen Alpha-Fehler des Typs I) =P (H ablehnen ₀ da H ₀ ist wahr),

Dies würde erreicht, wenn der Stichprobenmittelwert die kritischen Grenzen überschreitet.

=P (vorausgesetzt, H ₀ ist wahr) =alpha

Grafisch, es sieht wie folgt aus:

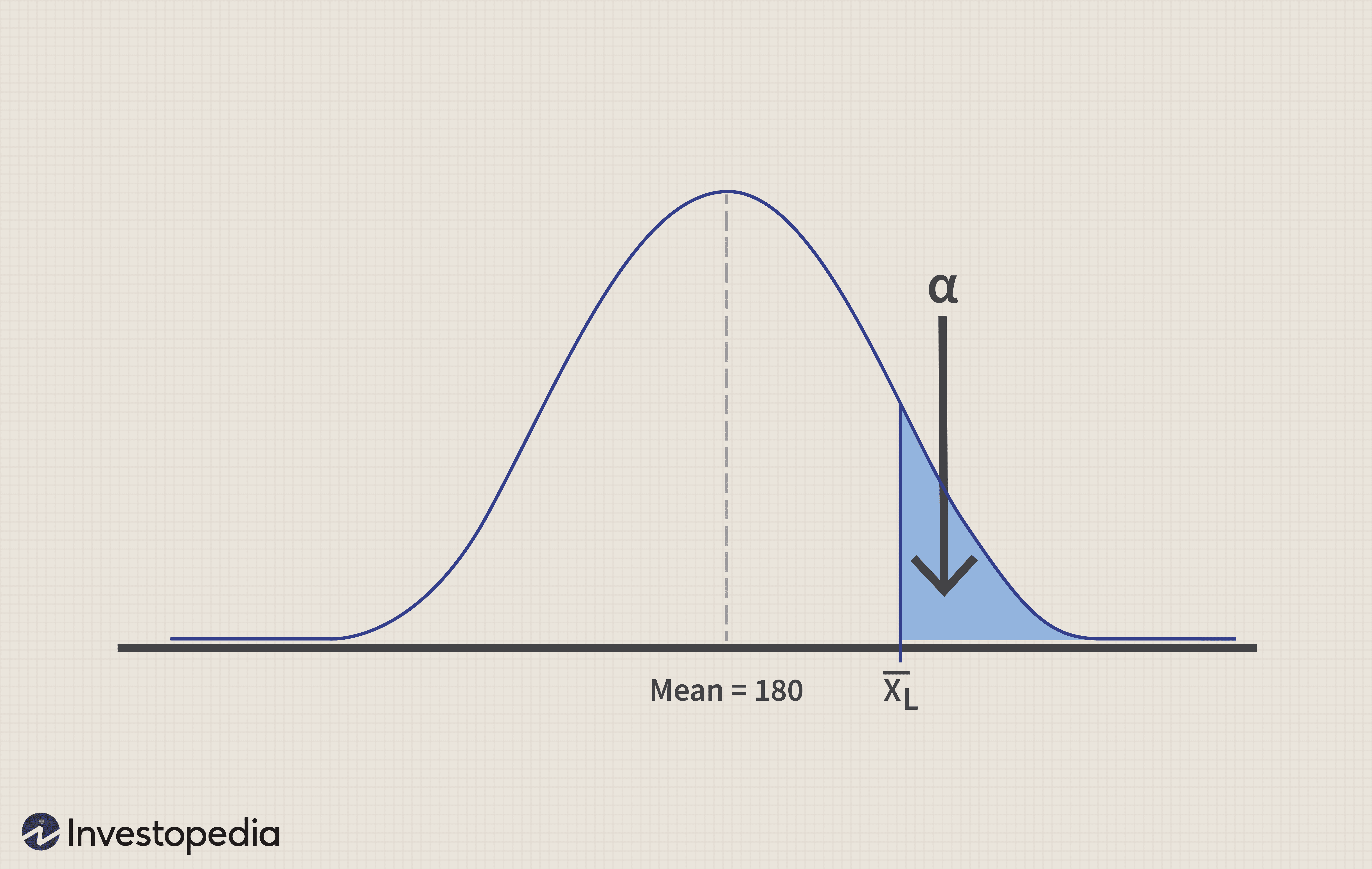
Unter Annahme von Alpha =0,05 (d. h. 5% Signifikanzniveau), Z _0,05 =1,645 (aus der Z-Tabelle oder Normalverteilungstabelle)

=> X _L =180 +1,645*(75/sqrt(300)) =187,12

Da der Stichprobenmittelwert (190) größer als der kritische Wert (187.12) ist, die Nullhypothese wird abgelehnt, und die Schlussfolgerung ist, dass die durchschnittliche monatliche Rendite tatsächlich mehr als 180 USD beträgt, Daher kann der Anleger in Erwägung ziehen, in dieses Programm zu investieren.

Methode 2:Standardisierte Teststatistiken verwenden

Man kann auch standardisierte Werte z verwenden.

Teststatistik, Z =(Stichprobenmittel – Bevölkerungsmittelwert) / (std-dev / sqrt (Anzahl der Stichproben).

Dann, der Ablehnungsbereich wird wie folgt:

Z=(190 – 180) / (75 / Quadrat (300)) =2,309

Unsere Ablehnungsregion auf einem Signifikanzniveau von 5% ist Z> Z _0,05 =1,645.

Da Z=2,309 größer als 1,645 ist, die Nullhypothese kann mit einer ähnlichen Schlussfolgerung wie oben erwähnt abgelehnt werden.

Methode 3: P-Wert-Berechnung

Unser Ziel ist es, P zu identifizieren (Stichprobenmittel>=190, wenn Mittel =180).

=P (Z>=(190-180) / (75 / Quadrat (300))

=P (Z>=2,309) =0,0084 =0,84%

Die folgende Tabelle zur Ableitung von p-Wert-Berechnungen kommt zu dem Schluss, dass es bestätigte Beweise dafür gibt, dass die durchschnittliche monatliche Rendite über 180 liegt:

p-Wert

Inferenz

weniger als 1%

Bestätigte Beweise unterstützende Alternativhypothese

zwischen 1% und 5%

Starker Beweis unterstützende Alternativhypothese

zwischen 5 % und 10 %

Schwache Beweise unterstützende Alternativhypothese

mehr als 10 %

Kein Beweis unterstützende Alternativhypothese

Beispiel 2

Ein neuer Börsenmakler (XYZ) behauptet, dass seine Maklergebühren niedriger sind als die Ihres aktuellen Börsenmaklers (ABC). Von einem unabhängigen Forschungsunternehmen verfügbare Daten weisen darauf hin, dass der Mittelwert und die Standardabweichung aller ABC-Broker-Kunden 18 USD und 6 USD betragen. bzw.

Eine Stichprobe von 100 Kunden von ABC wird gezogen und die Maklergebühren werden mit den neuen Sätzen des XYZ-Brokers berechnet. Wenn der Mittelwert der Stichprobe 18,75 $ beträgt und std-dev gleich ist ($6), Kann man Rückschlüsse auf den Unterschied in der durchschnittlichen Maklerrechnung zwischen ABC- und XYZ-Broker ziehen?

h ₀ :Nullhypothese:Mittelwert =18

h ₁ :Alternativhypothese:mean <> 18 (Das wollen wir beweisen.)

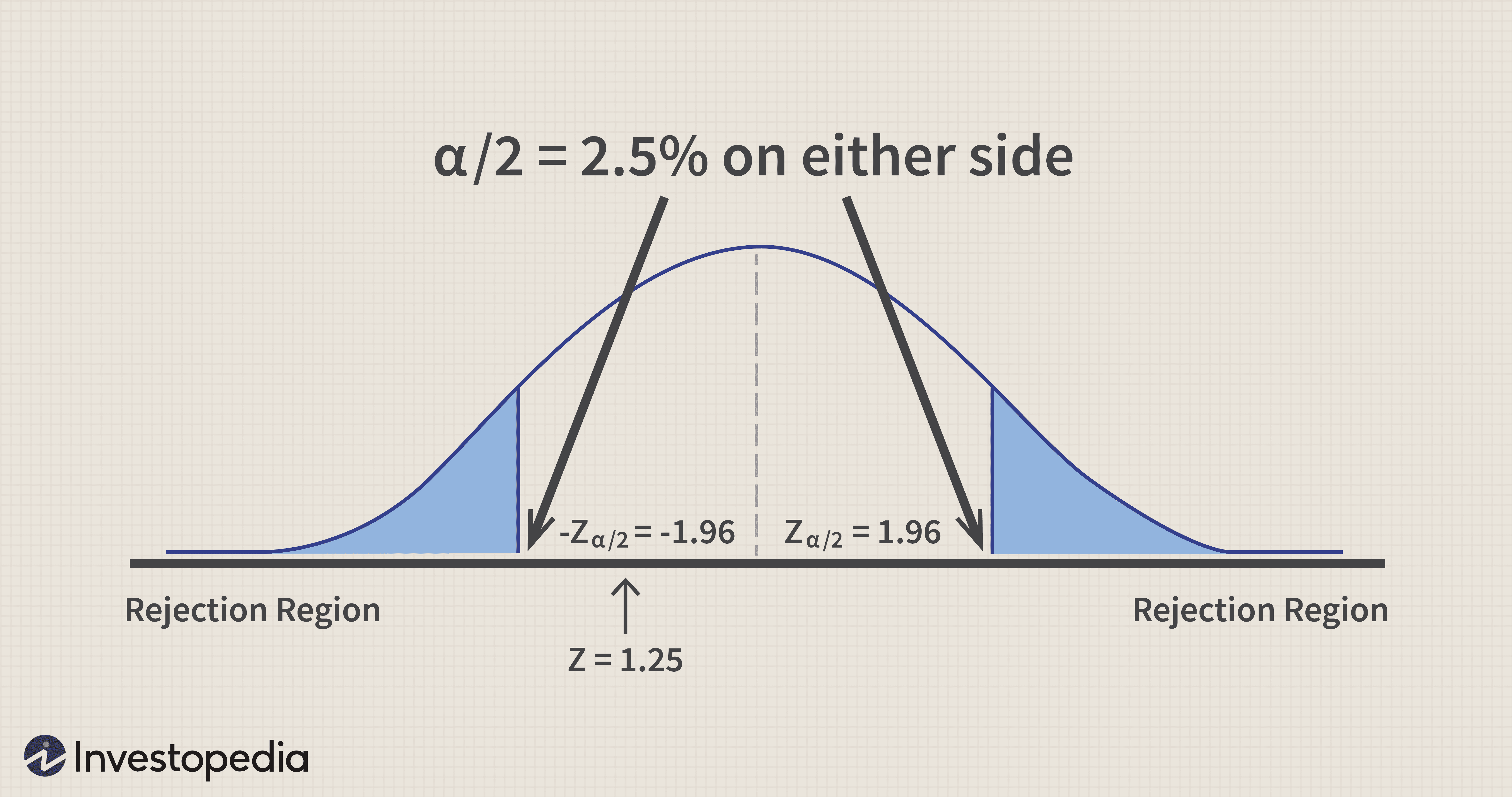
Ablehnungsbereich:Z <=- Z _2.5 und Z>=Z _2.5 (unter der Annahme eines Signifikanzniveaus von 5%, je 2,5 auf beiden Seiten teilen).

Z =(Stichprobenmittel – Mittelwert) / (std-dev / sqrt (Anzahl der Stichproben))

=(18,75 – 18) / (6/(Quadrat(100)) =1,25

Dieser berechnete Z-Wert liegt zwischen den beiden Grenzen definiert durch:

- Z _2.5 =-1,96 und Z _2.5 =1,96.

Dies kommt zu dem Schluss, dass es keine ausreichenden Beweise dafür gibt, dass es einen Unterschied zwischen den Tarifen Ihres bestehenden Brokers und des neuen Brokers gibt.

Alternative, Der p-Wert =P(Z<-1.25)+P(Z>1.25)

=2 * 0,1056 =0,2112 =21,12 % was größer als 0,05 oder 5 % ist, führt zum gleichen Schluss.

Grafisch, es wird durch Folgendes repräsentiert:

Kritikpunkte an der hypothetischen Testmethode:

• Eine auf Annahmen basierende statistische Methode
• Fehleranfällig wie im Detail in Bezug auf Alpha- und Beta-Fehler beschrieben
• Die Interpretation des p-Wertes kann mehrdeutig sein, führt zu verwirrenden Ergebnissen

Die Quintessenz

Hypothesentests ermöglichen es einem mathematischen Modell, eine Behauptung oder Idee mit einem bestimmten Konfidenzniveau zu validieren. Jedoch, wie die meisten statistischen Werkzeuge und Modelle, es ist an einige Einschränkungen gebunden. Die Verwendung dieses Modells für finanzielle Entscheidungen sollte kritisch hinterfragt werden, unter Berücksichtigung aller Abhängigkeiten. Alternative Methoden wie die Bayessche Inferenz sind für eine ähnliche Analyse ebenfalls eine Untersuchung wert.