Definition der T-Verteilung
Was ist eine T-Verteilung?
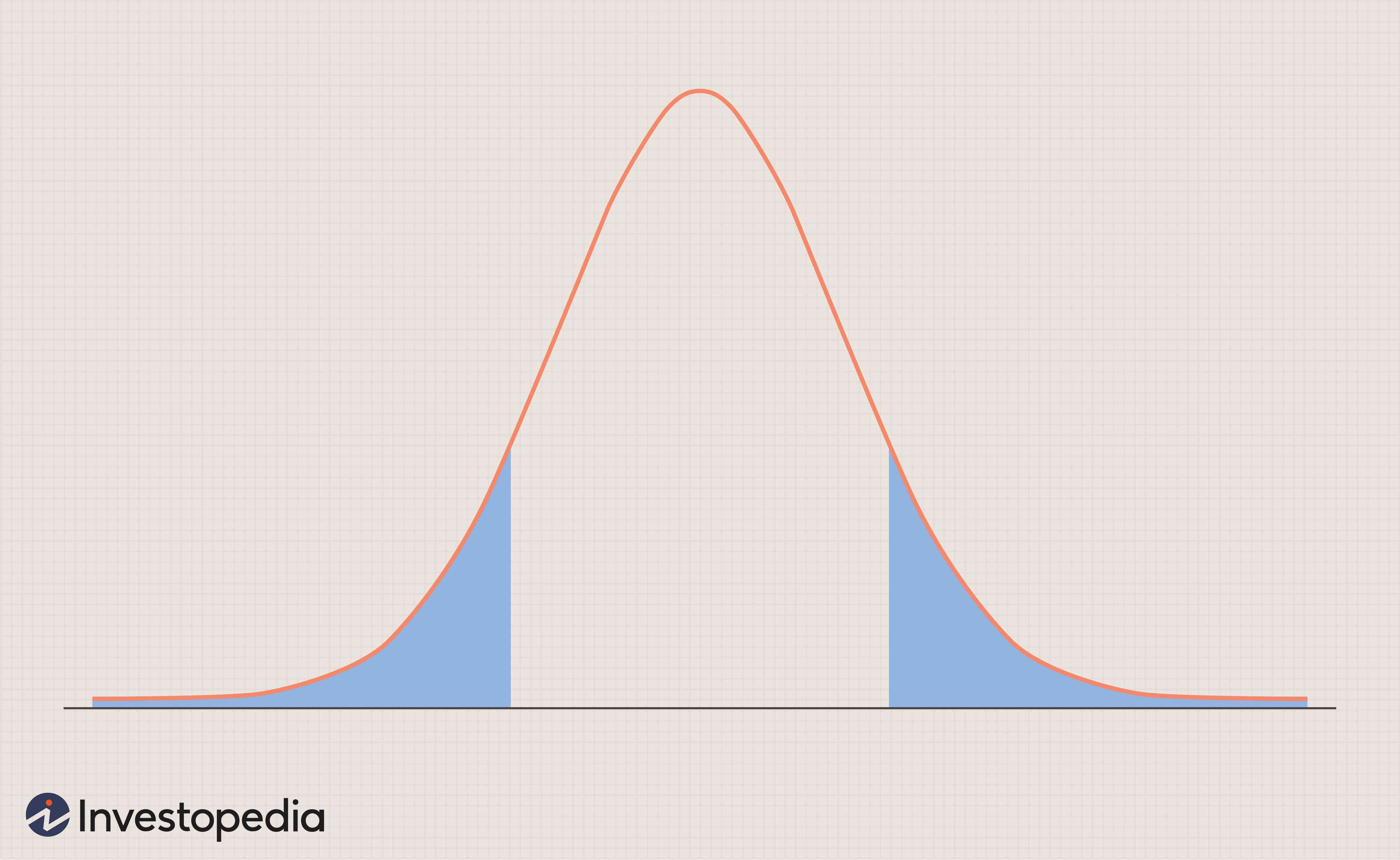
Die T-Verteilung, auch als Student-t-Verteilung bekannt, ist eine Art von Wahrscheinlichkeitsverteilung, die mit ihrer Glockenform der Normalverteilung ähnelt, jedoch stärkere Ausläufer hat. T-Verteilungen haben eine größere Chance für Extremwerte als Normalverteilungen, daher die dickeren Schwänze.
Die zentralen Thesen
- Die T-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung des z-Scores, wenn die geschätzte Standardabweichung im Nenner anstelle der wahren Standardabweichung verwendet wird.
- Die T-Verteilung, wie die Normalverteilung, ist glockenförmig und symmetrisch, aber es hat schwerere Schwänze, was bedeutet, dass es dazu neigt, Werte zu erzeugen, die weit von seinem Mittelwert abfallen.
- T-Tests werden in der Statistik verwendet, um die Signifikanz abzuschätzen.
Was sagt Ihnen eine T-Verteilung?
Die Schwanzschwere wird durch einen Parameter der T-Verteilung bestimmt, der als Freiheitsgrade bezeichnet wird, mit kleineren Werten, die schwerere Schwänze ergeben, und bei höheren Werten ähnelt die T-Verteilung einer Standardnormalverteilung mit einem Mittelwert von 0, und eine Standardabweichung von 1. Die T-Verteilung ist auch als "Student's T Distribution" bekannt.
Wenn eine Stichprobe von n Beobachtungen einer normalverteilten Grundgesamtheit mit Mittelwert M und Standardabweichung D entnommen wird, der Stichprobenmittelwert, m, und die Standardabweichung der Stichprobe, D, aufgrund der Zufälligkeit der Stichprobe von M und D abweichen.
Ein Z-Score kann mit der Standardabweichung der Grundgesamtheit als Z =(x – M)/D berechnet werden, und dieser Wert hat die Normalverteilung mit Mittelwert 0 und Standardabweichung 1. Aber wenn die geschätzte Standardabweichung verwendet wird, ein t-Score wird berechnet als T =(m – M)/{d/sqrt(n)}, der Unterschied zwischen d und D macht die Verteilung zu einer T-Verteilung mit (n - 1) Freiheitsgraden und nicht zur Normalverteilung mit Mittelwert 0 und Standardabweichung 1.
Beispiel für die Verwendung einer T-Verteilung
Nehmen Sie das folgende Beispiel für die Verwendung von t-Verteilungen in der statistischen Analyse. Zuerst, Denken Sie daran, dass ein Konfidenzintervall für den Mittelwert ein Wertebereich ist, aus den Daten berechnet, bedeutet, eine "Bevölkerung" zu erfassen. Dieses Intervall ist m +- t*d/sqrt(n), wobei t ein kritischer Wert aus der T-Verteilung ist.
Zum Beispiel, ein 95-%-Konfidenzintervall für die mittlere Rendite des Dow Jones Industrial Average in den 27 Handelstagen vor dem 11.09.2001, ist -0,33 %, (+/- 2,055) * 1,07 / Quadrat(27), ergibt eine (persistente) mittlere Rendite als eine Zahl zwischen -0,75 % und +0,09 %. Die Zahl 2.055, die Menge der zu korrigierenden Standardfehler, wird aus der T-Verteilung gefunden.
Da die T-Verteilung dickere Schwänze hat als eine Normalverteilung, es kann als Modell für finanzielle Renditen verwendet werden, die eine übermäßige Kurtosis aufweisen, was in solchen Fällen eine realistischere Berechnung des Value-at-Risk (VaR) ermöglicht.
Der Unterschied zwischen einer T-Verteilung und einer Normalverteilung
Normalverteilungen werden verwendet, wenn die Populationsverteilung als normal angenommen wird. Die T-Verteilung ähnelt der Normalverteilung, nur mit dickeren Schwänzen. Beide gehen von einer normalverteilten Population aus. T-Verteilungen haben eine höhere Kurtosis als normale Verteilungen. Die Wahrscheinlichkeit, sehr weit vom Mittelwert entfernte Werte zu erhalten, ist bei einer T-Verteilung größer als bei einer Normalverteilung.
Einschränkungen bei der Verwendung einer T-Verteilung
Die T-Verteilung kann die Genauigkeit relativ zur Normalverteilung verzerren. Ihr Manko entsteht nur, wenn es um vollkommene Normalität geht. Die T-Verteilung sollte nur verwendet werden, wenn die Standardabweichung der Grundgesamtheit nicht bekannt ist. Wenn die Standardabweichung der Grundgesamtheit bekannt ist und der Stichprobenumfang groß genug ist, Für bessere Ergebnisse sollte die Normalverteilung verwendet werden.
-
Candlestick-Definition
Was ist ein Kerzenständer? Ein Candlestick ist eine Art Preisdiagramm, das in der technischen Analyse verwendet wird und das Hoch, niedrig, offen, und Schlusskurse eines Wertpapiers für einen bestim
-
Todeskreuz Definition
Was ist ein Todeskreuz? Das Death Cross ist ein technisches Chartmuster, das das Potenzial für einen großen Ausverkauf anzeigt. Das Death Cross erscheint auf einem Chart, wenn der kurzfristige gleit
Aktienanalyse
-
Definition der Hypothekensteuerung Bei einigen Immobilienangeboten müssen potenzielle Käufer vom Verkäufer oder möglicherweise einem bestimmten Kreditgeber genehmigt werden, bevor sie kaufen können. Auf den ersten Blick, die Zustimmung...
-
Definition einer Versicherungsgarantie Viele Leute verwechseln die Begriffe Versicherung und Gewährleistung, „Manchmal verwenden sie sie austauschbar oder kombinieren sie miteinander, um ein Produkt zu beschreiben, das sie für ihr Zuhause ...