Was ist Portfoliovarianz?
Die Portfoliovarianz ist ein statistischer Wert, der den Streuungsgrad der Renditen eines Portfolios bewertet. Es ist ein wichtiges Konzept in der modernen Anlagetheorie. Auch wenn die statistische Kennzahl allein möglicherweise keine signifikanten Erkenntnisse liefert, Wir können die Standardabweichung berechnenStandardabweichungAus statistischer Sicht, Die Standardabweichung eines Datensatzes ist ein Maß für die Größe der Abweichungen zwischen den Werten der im Portfolio enthaltenen Beobachtungen unter Verwendung der Portfoliovarianz.

Bei der Berechnung der Portfoliovarianz wird nicht nur das Risiko einzelner Vermögenswerte berücksichtigt. nicht aktuell, körperlich, immateriell, Betriebs, und nicht betriebsbereit. Die richtige Identifizierung und auch die Korrelation zwischen jedem Paar von Vermögenswerten im Portfolio. Daher, Die statistische Varianz analysiert, wie sich Vermögenswerte innerhalb eines Portfolios tendenziell zusammen bewegen. Die allgemeine Regel der PortfoliodiversifikationDiversifikationDiversifikation ist eine Technik zur Allokation von Portfolioressourcen oder -kapital auf eine Vielzahl von Anlagen. Das Ziel der Diversifikation besteht darin, Verluste zu mindern, indem Vermögenswerte mit geringer oder negativer Korrelation untereinander ausgewählt werden.
Der Math for Corporate Finance-Kurs von CFI untersucht die finanzmathematischen Konzepte, die für die Finanzmodellierung erforderlich sind. Was ist Finanzmodellierung Die Finanzmodellierung wird in Excel durchgeführt, um die finanzielle Leistung eines Unternehmens vorherzusagen. Überblick über Financial Modeling, wie und warum man ein Modell baut.
Formel für Portfolioabweichung
Die Varianz für ein Portfolio bestehend aus zwei Assets wird nach folgender Formel berechnet:

Woher:
- w ich – das Gewicht des i-ten Vermögenswerts
- σ ich 2 – die Varianz des i-ten Vermögenswerts
- Bucht 1, 2 – die Kovarianz zwischen Aktiva 1 und 2
Beachten Sie, dass Kovarianz und Korrelation mathematisch zusammenhängen. Der Zusammenhang wird wie folgt ausgedrückt:

Woher:
- ρ 1, 2 – die Korrelation zwischen den Vermögenswerten 1 und 2
- Bucht 1, 2 – die Kovarianz zwischen Aktiva 1 und 2
- σ 1 – die Standardabweichung des Vermögenswerts 1
- σ 2 – die Standardabweichung des Vermögenswerts 2
Kenntnis der Beziehung zwischen Kovarianz und Korrelation, Wir können die Formel für die Portfoliovarianz wie folgt umschreiben:

Die Standardabweichung der Portfoliovarianz kann als Quadratwurzel der Portfoliovarianz berechnet werden:

Beachten Sie, dass für die Berechnung der Varianz für ein Portfolio, das aus mehreren Vermögenswerten besteht, Sie sollten den Faktor berechnen 2w ich w J Bucht i.j (oder 2w ich w J ρ ich , J, σ ich σ J ) für jedes mögliche Paar von Vermögenswerten im Portfolio.
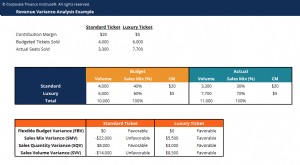
Beispiel für Portfolioabweichung
Fred hält ein Anlageportfolio, das aus drei Aktien besteht:Aktie A, Lager B, und Aktie C. Beachten Sie, dass Fred nur eine Aktie jeder Aktie besitzt. Informationen zu den einzelnen Aktien finden Sie in der folgenden Tabelle:

Fred möchte das Risiko des Portfolios anhand der Portfoliovarianz und der Portfoliostandardabweichung bewerten.
Zuerst, er muss die Gewichte jeder Aktie im Portfolio bestimmen. Dies kann erfolgen, indem der Gesamtwert jeder Aktie durch den Gesamtwert des Portfolios geteilt wird.

Zusätzlich, er muss die Korrelation zwischen jedem Aktienpaar kennen. Seine Berechnungen zeigen folgende Zusammenhänge:

Die Portfoliovarianz kann dann wie folgt berechnet werden:



Verwandte Lektüre
CFI bietet die Zertifizierung Financial Modeling &Valuation Analyst (FMVA)™Werden Sie zum zertifizierten Financial Modeling &Valuation Analyst (FMVA)®Die Zertifizierung zum Financial Modeling and Valuation Analyst (FMVA)® von CFI wird Ihnen dabei helfen, das Vertrauen zu gewinnen, das Sie für Ihre Finanzkarriere benötigen. Melden Sie sich noch heute an! Zertifizierungsprogramm für diejenigen, die ihre Karriere auf die nächste Stufe bringen möchten. Um weiter zu lernen und Ihre Karriere voranzutreiben, die folgenden CFI-Ressourcen sind hilfreich:
- Kurse zur Finanzmodellierung
- CorrelationCorrelationEine Korrelation ist ein statistisches Maß für die Beziehung zwischen zwei Variablen. Das Maß wird am besten in Variablen verwendet, die eine lineare Beziehung zueinander aufweisen. Die Anpassung der Daten kann visuell in einem Streudiagramm dargestellt werden.
- Negative KorrelationNegative KorrelationEine negative Korrelation ist eine Beziehung zwischen zwei Variablen, die sich in entgegengesetzte Richtungen bewegen. Mit anderen Worten, wenn Variable A zunimmt, Variable B nimmt ab. Eine negative Korrelation wird auch als inverse Korrelation bezeichnet. Siehe Beispiele, Diagramme und
- RegressionsanalyseRegressionsanalyseRegressionsanalyse ist ein Satz statistischer Methoden, die verwendet werden, um Beziehungen zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen zu schätzen.
Finanzen
-
 Was ist Portfolioplanung?
Was ist Portfolioplanung? Die Portfolioplanung ist der Prozess der strategischen Planung des Aufbaus eines Anlageportfolios. Das Anlageportfolio sollte die Risikotoleranz des Anlegers umfassen. Mehrere Faktoren bestimmen die H...
-
 Was ist ein Varianz-Swap?
Was ist ein Varianz-Swap? Variance Swap bezieht sich auf ein außerbörsliches Finanzderivat, das es dem Inhaber ermöglicht, auf die zukünftige Volatilität eines bestimmten Basiswerts zu spekulieren. Inhaber verwenden Variance S...