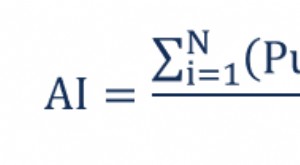Was ist der exponentiell gewichtete gleitende Durchschnitt (EWMA)?

Der Exponential Weighted Moving Average (EWMA) ist ein quantitatives oder statistisches Maß, das verwendet wird, um eine Zeitreihe zu modellieren oder zu beschreiben. Die EWMA ist im Finanzwesen weit verbreitet, die Hauptanwendungen sind die technische Analyse und die Volatilitätsmodellierung.

Der gleitende Durchschnitt ist so konzipiert, dass älteren Beobachtungen eine geringere Gewichtung gegeben wird. Mit zunehmendem Alter des Datenpunkts fallen die Gewichtungen exponentiell – daher der Name exponentiell gewichtet.

Die einzige Entscheidung, die ein Nutzer des EWMA treffen muss, ist der Parameter alphaAlphaAlpha ist ein Maß für die Wertentwicklung einer Anlage relativ zu einem geeigneten Referenzindex wie dem S&P 500. Ein Alpha von eins (der Basiswert ist null) zeigt, dass die Rendite auf die Investition während eines bestimmten Zeitraums übertraf den Gesamtmarktdurchschnitt um 1%. Der Parameter entscheidet, wie wichtig die aktuelle Beobachtung bei der Berechnung des EWMA ist. Je höher der Wert von Alpha, desto genauer verfolgt die EWMA die ursprüngliche Zeitreihe.

EWMA-Formel

Die nachfolgend beschriebene einfache mathematische Formulierung der EWMA:

Woher:

• Alpha =Das vom Benutzer festgelegte Gewicht
• R =Wert der Serie in der aktuellen Periode

Der EWMA ist eine rekursive Funktion, Das bedeutet, dass die aktuelle Beobachtung anhand der vorherigen Beobachtung berechnet wird. Die rekursive Eigenschaft des EWMA führt zu den exponentiell abfallenden Gewichten wie unten gezeigt:

Die obige Gleichung kann in Bezug auf ältere Gewichte umgeschrieben werden, Wie nachfolgend dargestellt:

Sie kann durch einen weiteren Zeitraum noch erweitert werden:

Der Prozess wird fortgesetzt, bis wir den Basisterm EWMA erreichen ₀ . Die Gleichung kann umgestellt werden, um zu zeigen, dass der EWMA _T ist der gewichtete Durchschnitt aller vorhergehenden Beobachtungen, wobei das Gewicht der Beobachtung r _t–k wird gegeben von:

Da Alpha zwischen 0 und 1 liegt, das Gewicht wird kleiner, wenn k größer wird. Mit anderen Worten, Wenn wir weiter in der Geschichte zurückgehen, das Gewicht wird kleiner. Die Tatsache ist in der folgenden Grafik dargestellt, die die Beobachtungsgewichte mit zunehmendem k für verschiedene Wahlen des Parameters alpha aufträgt.

N-Tage EWMA

Der EWMA kann für einen bestimmten Tagesbereich wie 20-Tage-EWMA oder 200-Tage-EWMA berechnet werden. Um den gleitenden Durchschnitt zu berechnen, wir müssen zuerst das entsprechende Alpha finden, was durch die folgende Formel gegeben ist:

Woher:

• n =Anzahl der Tage, für die der gleitende n-Tage-Durchschnitt berechnet wird

Zum Beispiel, das Alpha eines gleitenden 15-Tage-Durchschnitts wird durch 2/(15+1) angegeben, was bedeutet, dass Alpha 0,125 ist. Natürlich kürzer die Lookback-Periode – genauer, die EWMA – verfolgt die ursprüngliche Zeitreihe.

Anträge der EWMA

Technische Analyse

Der EWMA wird häufig in der technischen Analyse verwendet. Es darf nicht direkt verwendet werden, aber es wird in Verbindung mit anderen Indikatoren verwendet, um Handelssignale zu generieren. Ein bekanntes Beispiel ist der Negative Volume Index (NVI)Negative Volume Index (NVI)Der Negative Volume Index (NVI) ist ein technischer Indikator, der verwendet wird, um Trends in einem Markt zu erkennen. Wenn sich ein Trend auch bei sinkendem Handelsvolumen fortsetzt, Es ist ein starker Trend., die in Verbindung mit seinem EWMA verwendet wird. Ein Kaufsignal wird generiert, wenn der NVI seinen 250-Tage-EWMA überschreitet.

Der EWMA kann auch in einer einfachen Crossover-Strategie verwendet werden, wo ein Kaufsignal generiert wird, wenn der Preis den EWMA von oben kreuzt, und ein Verkaufssignal wird generiert, wenn der Preis den EWMA von unten kreuzt.

Eine weitere Anwendung des EWMA in der technischen Analyse besteht darin, dass er als Unterstützungs- oder Widerstandsniveau verwendet werden kann. Für diesen Zweck, es ist besser, längere gleitende Durchschnitte zu verwenden, normalerweise länger als ein gleitender 20-Tage-Durchschnitt.

Der folgende Chart zeigt den 5-Tage- und 15-Tage-EWMA für die Serie der MSFT-Aktienkurse:

Volatilitätsmodellierung

Der exponentiell gewichtete gleitende Durchschnitt wird häufig bei der Berechnung der Renditevolatilität im Risikomanagement verwendet. Es gibt verschiedene Methoden zur Berechnung der Renditevolatilität einer Preisreihe, wie die Methode der historischen Standardabweichung, die EWMA-Modelle, und das GARCH-Modell.

Die Standardabweichungsmethode gewichtet alle Beobachtungen gleich und unterschätzt häufig die Volatilität. Das GARCH-Modell ist ein komplexes statistisches Modell, das auf dem EWMA-Modell basiert. Das EWMA-Modell schafft die perfekte Balance zwischen Komplexität und Genauigkeit; somit, es ist ein sehr beliebter Ansatz zur Schätzung der Volatilität.

Die Volatilität kann mithilfe des EWMA wie folgt geschätzt werden:

1. Schritt 1 :Sortieren Sie den Abschlussprozess absteigend nach Datum, d.h., vom aktuellen zum ältesten Preis.
2. Schritt 2 :Wenn heute t ist, dann wird die Rendite am Tag t-1 berechnet als (S _T / S _t–1 ) wo ist _T ist der Preis des Tages t.
3. Schritt 3 :Berechnen Sie quadrierte Renditen, indem Sie die im vorherigen Schritt berechneten Renditen quadrieren.
4. Schritt 4 :Wählen Sie den EWMA-Parameter alpha. Für die Volatilitätsmodellierung der Wert von Alpha ist 0,8 oder größer. Die Gewichte werden durch ein einfaches Verfahren angegeben. Das erste Gewicht (1 – a); die folgenden Gewichtungen werden durch ein * Vorheriges Gewicht angegeben.
5. Schritt 5 :Multiplizieren Sie die quadrierten Renditen in Schritt 3 mit den entsprechenden Gewichtungen, die in Schritt 4 berechnet wurden. Summieren Sie das obige Produkt, um die EWMA-Varianz zu erhalten.
6. Schritt 6 :Schließlich, die Volatilität kann als Quadratwurzel der in Schritt 5 berechneten Varianz berechnet werden.

Die Volatilitätszahl wird dann verwendet, um Risikomaße wie den Value at Risk (VaR) zu berechnen. Es kann auch für die Optionsbewertung verwendet werden, wobei Volatilität ein Eingabeparameter für das Black-Scholes-Merton istBlack-Scholes-Merton-ModellDas Black-Scholes-Merton (BSM)-Modell ist ein Preismodell für Finanzinstrumente. Es wird zur Bewertung von Aktienoptionen verwendet. Formel.

Mehr Ressourcen

Um weiter zu lernen und Ihre Wissensdatenbank weiterzuentwickeln, Bitte erkunden Sie die zusätzlichen relevanten Ressourcen unten:

• Erweiterte technische AnalyseErweiterte technische AnalyseErweiterte technische Analyse beinhaltet in der Regel entweder die Verwendung mehrerer technischer Indikatoren oder eines ziemlich ausgeklügelten (d.h. Komplex) Indikator. "Anspruchsvoll"
• Double Exponential Moving Average (DEMA)Double Exponential Moving Average (DEMA)Double Exponential Moving Average (DEMA) sind eine Verbesserung gegenüber dem Exponential Moving Average (EMA), da sie mehr Gewicht auf
• Historische VolatilitätHistorische Volatilität (HV)Historische Volatilität, oder HV, ist ein statistischer Indikator, der die Renditeverteilung für einen bestimmten Wertpapier- oder Marktindex misst
• Value-at-Risk (VaR)Value-at-Risk (VaR)Value-at-Risk (VaR) schätzt das Risiko einer Anlage. Der VaR misst den potenziellen Verlust, der in einem Anlageportfolio über einen bestimmten Zeitraum eintreten könnte.