Bayes Theorem Definition
Was ist der Satz von Bayes?
Bayes' Satz, benannt nach dem britischen Mathematiker Thomas Bayes aus dem 18. ist eine mathematische Formel zur Bestimmung der bedingten Wahrscheinlichkeit. Bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit, dass ein Ergebnis eintritt, basierend auf einem früheren Ergebnis, das aufgetreten ist. Der Satz von Bayes bietet eine Möglichkeit, bestehende Vorhersagen oder Theorien (Aktualisierungswahrscheinlichkeiten) bei neuen oder zusätzlichen Beweisen zu revidieren. In der Finanzwelt, Der Satz von Bayes kann verwendet werden, um das Risiko der Kreditvergabe an potenzielle Kreditnehmer zu bewerten.
Der Satz von Bayes wird auch Bayes-Regel oder Bayes-Gesetz genannt und ist die Grundlage des Gebiets der Bayes-Statistik.
Die zentralen Thesen
- Der Satz von Bayes ermöglicht es Ihnen, vorhergesagte Wahrscheinlichkeiten eines Ereignisses zu aktualisieren, indem Sie neue Informationen einbeziehen.
- Der Satz von Bayes wurde nach dem Mathematiker Thomas Bayes aus dem 18. Jahrhundert benannt.
- Es wird häufig im Finanzwesen bei der Aktualisierung der Risikobewertung eingesetzt.
Das Theorem von Bayes verstehen
Anwendungen des Theorems sind weit verbreitet und nicht auf den Finanzbereich beschränkt. Als Beispiel, Der Satz von Bayes kann verwendet werden, um die Genauigkeit von medizinischen Testergebnissen zu bestimmen, indem die Wahrscheinlichkeit einer bestimmten Person mit einer Krankheit und die allgemeine Genauigkeit des Tests berücksichtigt werden. Der Satz von Bayes beruht auf der Einbeziehung von A-priori-Wahrscheinlichkeitsverteilungen, um A-posteriori-Wahrscheinlichkeiten zu erzeugen. Vorherige Wahrscheinlichkeit, in Bayes'scher statistischer Inferenz, ist die Wahrscheinlichkeit eines Ereignisses, bevor neue Daten gesammelt werden. Dies ist die beste rationale Einschätzung der Wahrscheinlichkeit eines Ergebnisses basierend auf dem aktuellen Wissen, bevor ein Experiment durchgeführt wird. Posterior-Wahrscheinlichkeit ist die revidierte Wahrscheinlichkeit, dass ein Ereignis unter Berücksichtigung neuer Informationen eintritt. Die Posterior-Wahrscheinlichkeit wird berechnet, indem die A-priori-Wahrscheinlichkeit unter Verwendung des Bayes-Theorems aktualisiert wird. Statistisch gesehen, die Posterior-Wahrscheinlichkeit ist die Wahrscheinlichkeit des Eintretens von Ereignis A, vorausgesetzt, dass Ereignis B eingetreten ist.
Der Satz von Bayes gibt somit die Wahrscheinlichkeit eines Ereignisses basierend auf neuen Informationen an, d. oder kann verwandt sein, zu dieser Veranstaltung. Die Formel kann auch verwendet werden, um zu sehen, wie die Wahrscheinlichkeit des Eintretens eines Ereignisses durch hypothetische neue Informationen beeinflusst wird. Angenommen, die neuen Informationen werden sich als wahr herausstellen. Zum Beispiel, sagen wir, eine einzelne Karte wird aus einem vollständigen Deck von 52 Karten gezogen. Die Wahrscheinlichkeit, dass die Karte ein König ist, ist vier geteilt durch 52, das entspricht 1/13 oder ungefähr 7,69 %. Denken Sie daran, dass es vier Könige im Deck gibt. Jetzt, Angenommen, es wird aufgedeckt, dass die ausgewählte Karte eine Bildkarte ist. Die Wahrscheinlichkeit, dass die ausgewählte Karte ein König ist, da es sich um eine Bildkarte handelt, ist vier geteilt durch 12, oder ungefähr 33,3%, da es 12 Bildkarten in einem Deck gibt.
Formel für den Satz von Bayes
Beispiele für den Satz von Bayes
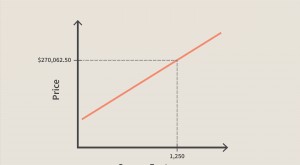
Unten sind zwei Beispiele für Bayes' Theorem, in denen das erste Beispiel zeigt, wie die Formel in einem Aktieninvestitionsbeispiel unter Verwendung von Amazon.com Inc. (AMZN) abgeleitet werden kann. Das zweite Beispiel wendet den Satz von Bayes auf die Arzneimittelprüfung an.
Ableitung der Bayes-Theorem-Formel
Der Satz von Bayes folgt einfach aus den Axiomen der bedingten Wahrscheinlichkeit. Bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit eines Ereignisses, wenn ein anderes Ereignis eingetreten ist. Zum Beispiel, eine einfache Wahrscheinlichkeitsfrage könnte lauten:"Wie hoch ist die Wahrscheinlichkeit, dass der Aktienkurs von Amazon.com fällt?" Die bedingte Wahrscheinlichkeit geht in dieser Frage noch einen Schritt weiter, indem sie fragt:"Wie groß ist die Wahrscheinlichkeit, dass der AMZN-Aktienkurs fällt? da der Dow Jones Industrial Average (DJIA) Index früher gefallen ist?"
Die bedingte Wahrscheinlichkeit von A, dass B passiert ist, kann wie folgt ausgedrückt werden:
Wenn A ist:"AMZN-Preis fällt", dann ist P(AMZN) die Wahrscheinlichkeit, dass AMZN fällt; und B ist:"DJIA ist schon down, " und P(DJIA) ist die Wahrscheinlichkeit, dass der DJIA gefallen ist; dann lautet der bedingte Wahrscheinlichkeitsausdruck als "Die Wahrscheinlichkeit, dass AMZN bei einem Rückgang des DJIA sinkt, ist gleich der Wahrscheinlichkeit, dass der AMZN-Preis sinkt und der DJIA über die Wahrscheinlichkeit eines Rückgangs sinkt den DJIA-Index.
P(AMZN|DJIA) =P(AMZN und DJIA) / P(DJIA)
P(AMZN und DJIA) ist die Wahrscheinlichkeit von beide A und B auftreten. Dies entspricht auch der Wahrscheinlichkeit, dass A auftritt, multipliziert mit der Wahrscheinlichkeit, dass B auftritt, wenn A auftritt. ausgedrückt als P(AMZN) x P(DJIA|AMZN). Die Tatsache, dass diese beiden Ausdrücke gleich sind, führt zum Satz von Bayes, was geschrieben ist als:
wenn, P(AMZN und DJIA) =P(AMZN) x P(DJIA|AMZN) =P(DJIA) x P(AMZN|DJIA)
dann, P(AMZN|DJIA) =[P(AMZN) x P(DJIA|AMZN)] / P(DJIA).
Wobei P(AMZN) und P(DJIA) die Wahrscheinlichkeiten sind, dass Amazon und der Dow Jones fallen, ohne Rücksicht aufeinander.
Die Formel erklärt die Beziehung zwischen der Wahrscheinlichkeit der Hypothese, bevor die Beweise gesehen werden, dass P(AMZN), und die Wahrscheinlichkeit der Hypothese nach Erhalt des Beweises P(AMZN|DJIA), eine Hypothese für Amazon gegeben Beweise im Dow.
Numerisches Beispiel des Satzes von Bayes
Als Zahlenbeispiel ist Stellen Sie sich vor, es gibt einen Drogentest, der zu 98% genau ist, Das bedeutet, dass es in 98 % der Fälle ein wahrhaft positives Ergebnis für jemanden zeigt, der die Droge konsumiert, und in 98 % der Fälle, ein wahrhaft negatives Ergebnis für Nichtkonsumenten der Droge. Nächste, Nehmen Sie an, dass 0,5% der Menschen das Medikament konsumieren. Wenn eine nach dem Zufallsprinzip ausgewählte Person positiv auf das Medikament getestet wird, ob die Wahrscheinlichkeit, dass die Person tatsächlich ein Konsument der Droge ist, kann durch folgende Berechnung durchgeführt werden.
(0,98 x 0,005) / [(0,98 x 0,005) + ((1 - 0,98) x (1 - 0,005))] =0,0049 / (0,0049 + 0,0199) =19,76 %
Der Satz von Bayes zeigt, dass selbst wenn eine Person in diesem Szenario positiv getestet wurde, es ist tatsächlich viel wahrscheinlicher, dass die Person kein Konsument der Droge ist.
Finanzen
-
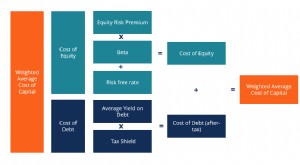 Definition von WACC
Definition von WACC Die gewichteten durchschnittlichen Kapitalkosten (WACC) eines Unternehmens stellen seine gemischten Kapitalkosten dar. Bevor ein Unternehmen Gewinne erzielen kann, sie muss zumindest ausreichende Einn...
-
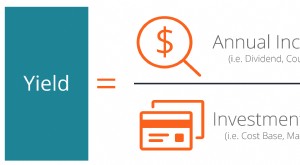 Was ist Ertrag (Definition)?
Was ist Ertrag (Definition)? Die Rendite ist definiert als eine reine Einkommensrendite (ohne KapitalgewinneCapital Gains YieldDie Kapitalgewinnrendite (CGY) ist die Kurssteigerung einer Anlage oder eines Wertpapiers, ausgedrückt...