Was ist eine Korrelation?

Eine Korrelation ist ein statistisches Maß für die Beziehung zwischen zwei Variablen. Das Maß wird am besten in Variablen verwendet, die eine lineare Beziehung zueinander aufweisen. Die Anpassung der Daten kann visuell in einem Streudiagramm dargestellt werden. Mit einem Streudiagramm, Wir können allgemein die Beziehung zwischen den Variablen beurteilen und feststellen, ob sie korreliert sind oder nicht.

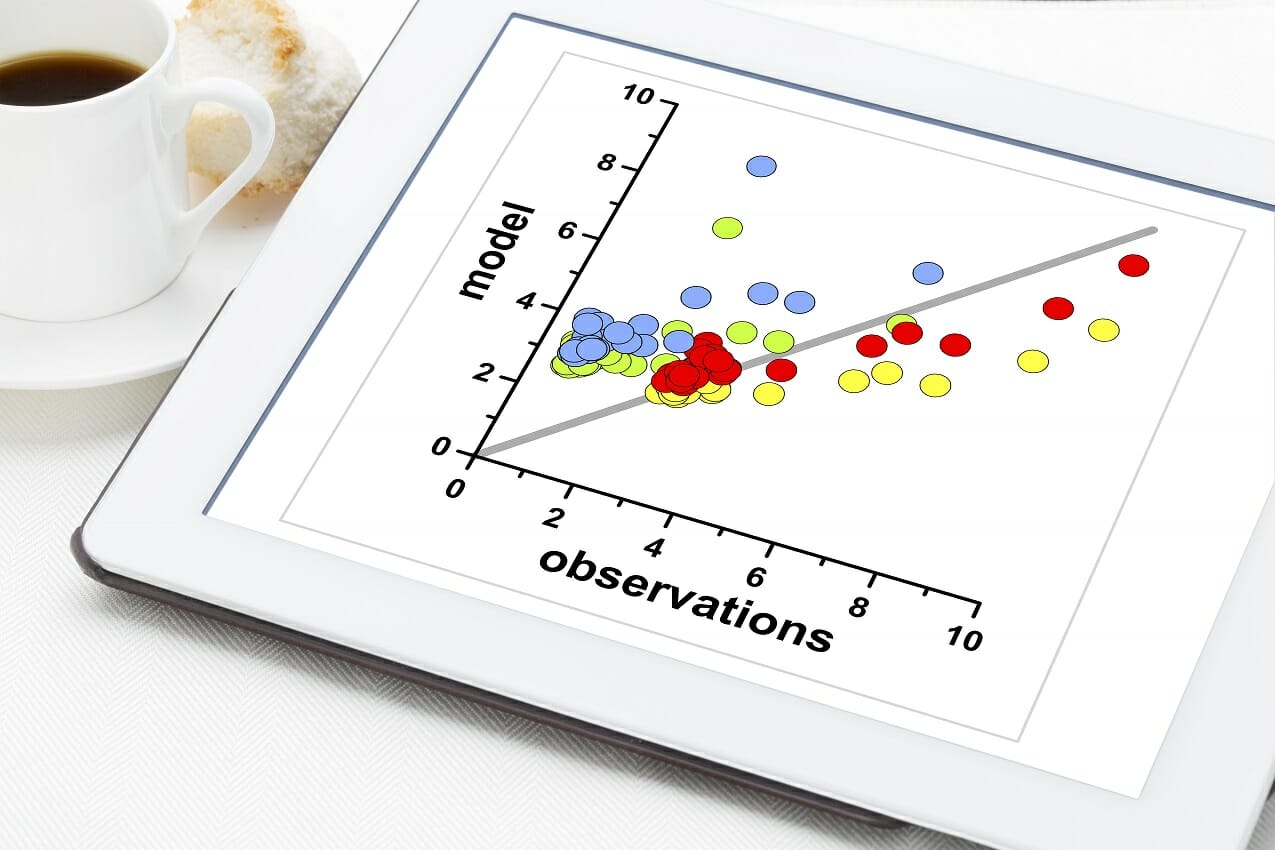
Der Korrelationskoeffizient ist ein Wert, der die Stärke der Beziehung zwischen Variablen angibt. Der Koeffizient kann beliebige Werte von -1 bis 1 annehmen. Die Interpretationen der Werte sind:

• -1: Perfekte negative Korrelation. Die Variablen neigen dazu, sich in entgegengesetzte Richtungen zu bewegen (d. h. wenn eine Variable zunimmt, die andere Variable nimmt ab).
• 0: Keine Korrelation. Die Variablen haben keine Beziehung zueinander.
• 1: Perfekte positive Korrelation. Die Variablen tendieren dazu, sich in die gleiche Richtung zu bewegen (d. h. wenn eine Variable zunimmt, die andere Variable nimmt ebenfalls zu).

Eine der Hauptanwendungen des Konzepts im Finanzbereich liegt im PortfoliomanagementPortfolio Management KarriereprofilPortfolio Management verwaltet Investitionen und Vermögenswerte für Kunden, zu denen Pensionskassen gehören, Banken, Hedgefonds, Family Offices bzw. Der Portfoliomanager ist dafür verantwortlich, den richtigen Vermögensmix und die richtige Anlagestrategie aufrechtzuerhalten, die den Bedürfnissen des Kunden entsprechen. Gehalt, Fähigkeiten, . Ein gründliches Verständnis dieses statistischen Konzepts ist für eine erfolgreiche Portfoliooptimierung unerlässlich.

Korrelation und Kausalität

Korrelation darf nicht mit Kausalität verwechselt werden. Der berühmte Ausdruck „Korrelation bedeutet nicht Kausalität“ ist entscheidend für das Verständnis der beiden statistischen Konzepte.

Wenn zwei Variablen korreliert sind, es bedeutet nicht, dass eine Variable die Änderungen einer anderen Variable verursacht. Korrelation bewertet nur Beziehungen zwischen Variablen, und es kann verschiedene Faktoren geben, die zu den Beziehungen führen. Kausalität kann ein Grund für den Zusammenhang sein, aber es ist nicht die einzige mögliche Erklärung.

Der Math for Corporate Finance-Kurs von CFI untersucht die Konzepte der Finanzmathematik, die für die Finanzmodellierung erforderlich sind.Was ist FinanzmodellierungFinanzmodellierung wird in Excel durchgeführt, um die finanzielle Leistung eines Unternehmens vorherzusagen. Überblick über Financial Modeling, wie und warum man ein Modell baut.

Wie finde ich die Korrelation?

Der Korrelationskoeffizient, der die Stärke der Beziehung zwischen zwei Variablen angibt, kann mit der folgenden Formel ermittelt werden:

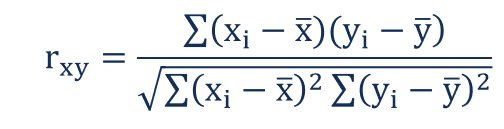
Woher:

• R _xy – der Korrelationskoeffizient der linearen Beziehung zwischen den Variablen x und y
• x _ich – die Werte der x-Variablen in einer Stichprobe
• x – der Mittelwert der Werte der x-Variablen
• ja _ich – die Werte der y-Variablen in einer Stichprobe
• Ȳ – der Mittelwert der Werte der y-Variablen

Um den Korrelationskoeffizienten mit der obigen Formel zu berechnen, Sie müssen die folgenden Schritte ausführen:

1. Erhalten Sie eine Datenstichprobe mit den Werten der x-Variablen und y-Variablen.
2. Berechnen Sie die Mittelwerte (Durchschnitte) x für die x-Variable und Ȳ für die y-Variable.
3. Für die x-Variable gilt:subtrahieren Sie den Mittelwert von jedem Wert der x-Variablen (nennen wir diese neue Variable „a“). Machen Sie dasselbe für die y-Variable (nennen wir diese Variable „b“).
4. Multiplizieren Sie jeden a-Wert mit dem entsprechenden b-Wert und ermitteln Sie die Summe dieser Multiplikationen (der Endwert ist der Zähler in der Formel).
5. Quadriere jeden a-Wert und berechne die Summe des Ergebnisses
6. Finden Sie die Quadratwurzel des im vorherigen Schritt erhaltenen Werts (dies ist der Nenner in der Formel).
7. Teilen Sie den erhaltenen Wert in Schritt 4 durch den erhaltenen Wert in Schritt 7 .

Sie sehen, dass die manuelle Berechnung des Korrelationskoeffizienten ein äußerst mühsamer Prozess ist, insbesondere wenn die Datenstichprobe groß ist. Jedoch, Es gibt viele Softwaretools, mit denen Sie bei der Berechnung des Koeffizienten Zeit sparen können. Die CORREL-Funktion CORREL-FunktionDie CORREL-Funktion ist unter Excel-Statistikfunktionen kategorisiert. Es berechnet den Korrelationskoeffizienten zwischen zwei Variablen. Als Finanzanalyst Die CORREL-Funktion ist sehr nützlich, wenn wir die Korrelation zwischen zwei Variablen finden möchten, z.B., Die Korrelation zwischen ain Excel ist eine der einfachsten Möglichkeiten, die Korrelation zwischen zwei Variablen für einen großen Datensatz schnell zu berechnen.

Beispiel für Korrelation

John ist Investor. Sein Portfolio bildet in erster Linie die Performance des S&P 500 ab und John möchte die Aktie von Apple Inc. aufnehmen. Bevor er Apple in sein Portfolio aufnimmt, er möchte die Korrelation zwischen der Aktie und dem S&P 500 beurteilen. S&P ist ein Marktführer, um sicherzustellen, dass das Hinzufügen der Aktie das systematische Risiko seines Portfolios nicht erhöht. Um den Koeffizienten zu finden, John sammelt die folgenden Preise für die letzten fünf Jahre ( Schritt 1 ):

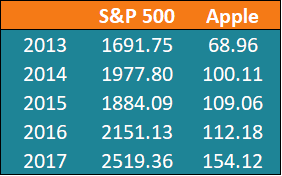
Verwenden Sie die obige Formel, John kann die Korrelation zwischen den Kursen des S&P 500 Index und Apple Inc.

Zuerst, John berechnet die Durchschnittskurse jedes Wertpapiers für die angegebenen Zeiträume ( Schritt 2 ):

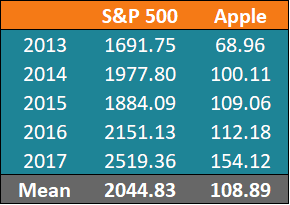
Nach der Berechnung der Durchschnittspreise, Wir können die anderen Werte finden. Eine Zusammenfassung der Berechnungen finden Sie in der folgenden Tabelle:

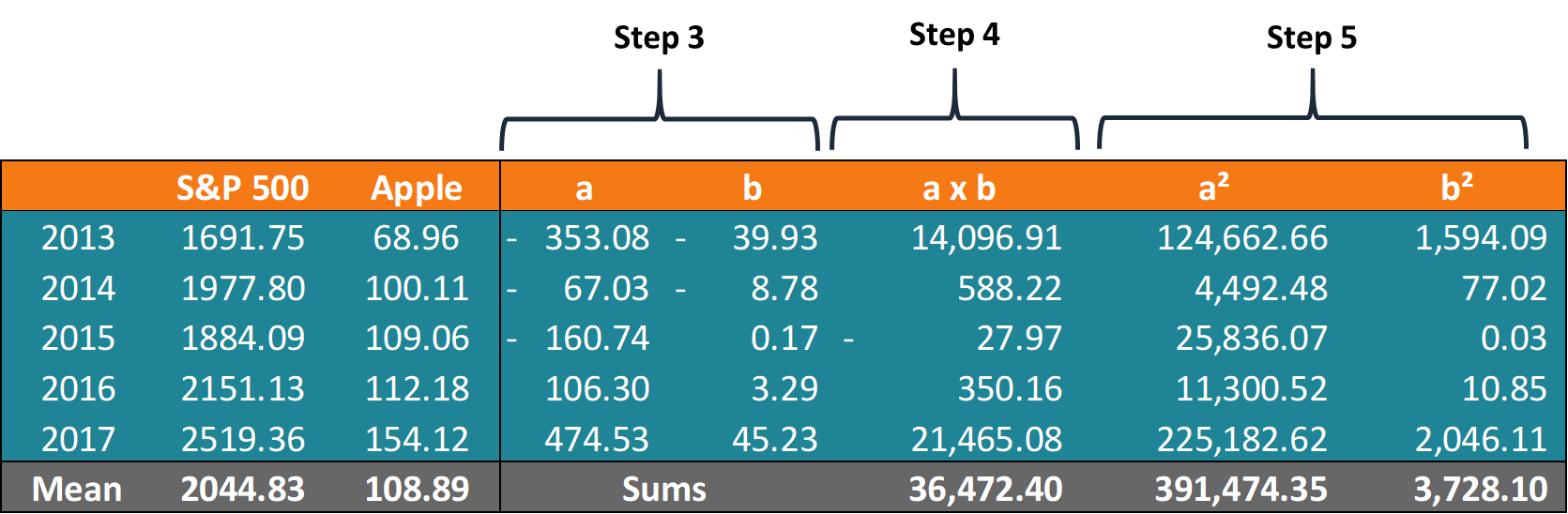
Mit den erhaltenen Zahlen, John kann den Koeffizienten berechnen:

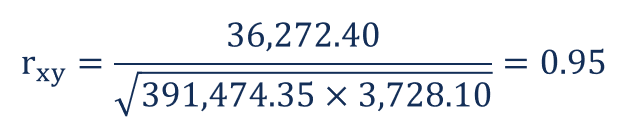
Der Koeffizient zeigt an, dass die Kurse des S&P 500 und der Apple Inc. eine hohe positive Korrelation aufweisen. Dies bedeutet, dass sich ihre jeweiligen Preise tendenziell in die gleiche Richtung bewegen. Deswegen, Apple in sein Portfolio aufzunehmen würde, in der Tat, das systematische Risiko erhöhen.

Verwandte Lektüre

Vielen Dank, dass Sie die Erklärung von CFI zur Korrelation gelesen haben. CFI ist der offizielle Anbieter des Financial Modeling and Valuation Analyst (FMVA)™Werden Sie ein Certified Financial Modeling &Valuation Analyst (FMVA)®Die Zertifizierung des Financial Modeling and Valuation Analyst (FMVA)® von CFI wird Ihnen helfen, das Vertrauen zu gewinnen, das Sie in Ihre Finanzen brauchen Werdegang. Melden Sie sich noch heute an! Zertifizierungsprogramm, entwickelt, um jeden in einen Weltklasse-Finanzanalysten zu verwandeln.

Um Ihr Wissen über Finanzanalysen weiter zu lernen und weiterzuentwickeln, Wir empfehlen dringend die folgenden zusätzlichen CFI-Ressourcen:

• Anchoring BiasAnchoring BiasAnchoring Bias tritt auf, wenn Menschen sich bei Entscheidungen zu sehr auf bereits vorhandene Informationen oder die ersten Informationen verlassen, die sie finden. Anker sind ein wichtiges Konzept in der Behavioral Finance.
• Dynamische FinanzanalyseDynamische FinanzanalyseIn diesem Handbuch erfahren Sie, wie Sie dynamische Finanzanalysen in Excel mit erweiterten Formeln und Funktionen durchführen. INDEX, SPIEL, und INDEX MATCH MATCH-Funktionen, Kombinieren von ZELLE, ANZAHL, MID und OFFSET in einer Formel. Wenn benutzt, diese Excel-Funktionen machen Ihre Bilanzanalyse dynamischer
• HypothesentestenHypothesentestsHypothesentests ist eine Methode der statistischen Inferenz. Es wird verwendet, um zu testen, ob eine Aussage zu einem Populationsparameter richtig ist. Hypothesentest
• Poisson-VerteilungPoisson-VerteilungDie Poisson-Verteilung ist ein Werkzeug, das in der Wahrscheinlichkeitstheorie-Statistik verwendet wird, um das Ausmaß der Abweichung von einer bekannten durchschnittlichen Auftretensrate vorherzusagen. innerhalb